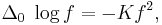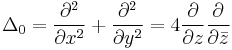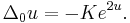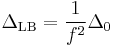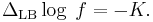Liouville's equation

For Liouville's equation in dynamical systems, see Liouville's theorem (Hamiltonian).

For Liouville's equation in quantum mechanics, see Density operator#Von Neumann equation.

In differential geometry, Liouville's equation, named after Joseph Liouville, is the nonlinear ordinary differential equation satisfied by the conformal factor f of a metric $f^2 (dx^2 %2B dy^2)$ on a surface of constant Gaussian curvature K:

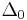$\Delta_0 \;\log f = -K f^2,$

where $\Delta_0$ is the flat Laplace operator.

$\Delta_0 = \frac{\partial^2}{\partial x^2} %2B\frac{\partial^2}{\partial y^2} = 4 \frac{\partial}{\partial z} \frac{\partial}{\partial \bar z}$

Liouville's equation typically appears in differential geometry books under the heading isothermal coordinates. This term refers to the coordinates x,y, while f can be described as the conformal factor with respect to the flat metric (sometimes the square 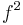$f^2$ is referred to as the conformal factor, instead of f itself).

Replacing f using 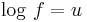$\log \,f = u$ , we obtain another commonly found form of the same equation:

$\Delta_0 u = - K e^{2u}.$

Laplace-Beltrami operator

In a more invariant fashion, the equation can be written in terms of the intrinsic Laplace-Beltrami operator

$\Delta_{\mathrm{LB}} = \frac{1}{f^2} \Delta_0$

as follows:

$\Delta_{\mathrm{LB}}\log\; f = -K.$

Relation to Gauss–Codazzi equations

Liouville's equation is a consequence of the Gauss–Codazzi equations when the metric is written in isothermal coordinates.

General solution

In a simply connected domain $\Omega$ the general solution is given by

$u(z,\bar z) = \frac{1}{2} \ln \left( 4 \frac{ |d f(z)/ d z|^2 }{ ( 1%2BK |f(z)|^2)^2 } \right)$

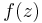where $f(z)$ is a locally univalent meromorphic function and 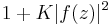$1%2BK |f(z)|^2$ when $K<0$ .